Fast Polynomial Multiplication Using the Fourier Transform Algorithm
The Fourier transform is a relatively difficult to understand algorithm, whether the fast version (FFT) or the slow one, based directly on the mathematical definition. I'll give you an overview of the algorithm and how it can be used, specifically for polynomial multiplication, one of the classic applications.
Why polynomial multiplication? While it may not be the most relevant application of the Fourier transform, it's one of the easiest to understand. It can serve as an entry point to understand other more complex applications of Fourier analysis.
This article isn't meant to cover the theory regarding Fourier analysis nor demonstrate every single theorem or concept formally. I kept it simple and informal on purpose.
Multiplicating Polynomials Is Equivalent to Convolution
First, let's talk about the concept of convolutions. An easy way to understand what a convolution is is by using polynomial multiplication as an example, which is in itself a convolution. We'll specifically be using discrete convolutions, as opposed to convolutions that operate on continuous functions.
Let's say we have two polynomials:
$$P(x) = -6 + 2x + 4x^2$$
$$Q(x) = 2 - x + 8x^2$$
The multiplication \(P(x)Q(x)\) will give us:
$$P(x)Q(x) = -12 + 10x - 42x^2 + 12x^3 + 32x^4$$
Now let's say instead of polynomials, we use the sequence of coefficients, such as:
$$u = (-6, 2, 4)$$
$$v = (2, -1, 8)$$
We can then apply the convolution operator (\(*\)), which gives us the same sequence of coefficients as when we multiplied the polynomials earlier:
$$u * v = (-12, 10, -42, 12, 32)$$
You can verify this result in Python:
import numpy as np np.convolve([-6, 2, 4], [2, -1, 8]) # Returns: # array([-12, 10, -42, 12, 32])
Therefore, convolution and polynomial multiplication can (for practical purposes) be considered as the same operation.
What Is the Discrete Fourier Transform
Explaining the theory behind the Fourier transform in full detail is out of the scope of this article, but here's a quick definition (check Wikipedia for more details):
Given a sequence of \(N\) numbers, \((x_0, x_1, ... x_{N-1})\), applying the Fourier transform returns another sequence \((X_0, X_1, ..., X_{N-1})\), defined by the following formula:
$$X_k = \sum_{n=0}^{N-1} x_n e^{-i2\pi \frac{k}{N}n}$$
One thing to note is that this formula resembles a polynomial evaluated using a complex number.
For instance, let's say our sequence is \((5, 4, 2)\). If we expand the element \(X_1\) we get:
$$X_1 = 5\ e^{(-i2\pi \frac{1}{3})0} + 4\ e^{(-i2\pi \frac{1}{3})1} + 2\ e^{(-i2\pi \frac{1}{3})2}
\\
= 5 + 4\ e^{-i2\pi \frac{1}{3}} + 2\ e^{(-i2\pi \frac{1}{3})2}$$
On a close inspection, you'll notice this is the same as the polynomial \(P(x) = 5 + 4x + 2x^2\) evaluated on \(x = e^{-i2\pi \frac{1}{3}}\).
Generalizing, \(X_k = P(e^{-i2\pi \frac{k}{N}})\) that is, the \(k\)-th element of the resulting Fourier transform sequence is the polynomial evaluated on the complex number \(e^{-i2\pi \frac{k}{N}}\), which depends both on \(k\) (current element index) and \(N\) (total sequence length). If the two sequences to convolve only have integer values, then the resulting sequence will only have elements with a real part.
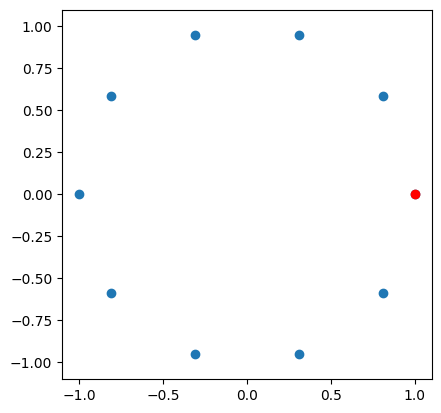
For \(N = 10\), if we plot the values for \(k = 0, 1, .., 9\) on the complex plane, we get the following. The red point is the value for \(k = 0\). The takeaway here is that each element of the resulting sequence is equal to the polynomial being evaluated on each of the complex values that lie on the circle of radius \(1\), with the circle being divided into \(N\) equal parts (i.e., the angle between each consecutive point is the same). Points are traversed in order when building the sequence (in most computer implementations, the result will have some precision issues since trigonometric functions need to be used.)
This can help understand the relationship between Fourier transforms, convolutions, and evaluation of polynomial functions; however, I'm not going to go further into this topic.
If you have trouble understanding this, then at least know that the Fourier transform of a sequence outputs another sequence.
Algorithm Overview
Let's explore how we can use the Fourier transform to find the convolution of two sequences.
The convolution theorem states that if we have two sequences and obtain the Fourier transform of both, we can simply multiply each item with its corresponding item in the other sequence (i.e., multiplication of elements in the same position).
This is called element-wise (or point-wise) multiplication and can be done in \(\mathcal{O}(n)\), as opposed to the convolution operation, which can only be done in \(\mathcal{O}(n^2)\) using the vanilla naïve algorithm.
Then, we simply apply the inverse Fourier transform to the result obtained in the previous step, and this would yield the convolution of the two original sequences. This is the final result we are looking for.
Both the Fourier transform and its inverse can be computed in \(\mathcal{O}(n\ log\ n)\) by using the Fast Fourier Transform. In this article, I present both the \(\mathcal{O}(n^2)\) (which is a lot easier to understand) and the faster \(\mathcal{O}(n\ log\ n)\) version of it.
Since the point-wise multiplication has linear time complexity, and computing the Fourier transform (and its inverse) has \(\mathcal{O}(n\ log\ n)\) time complexity, then the final algorithm has \(\mathcal{O}(n\ log\ n)\) time as well.
Simple Implementation in Python
Here, we will compute the Fourier transform using the naïve algorithm. To compute the Fourier transform, you could use the mathematical definition introduced earlier, but an easier way is to use the DFT matrix (discrete Fourier transform matrix).
The DFT matrix is a transformation matrix containing the complex numbers described above conveniently organized in appropriate positions. Applying this transformation to a sequence yields its Fourier transform. Since this matrix is always invertible, we get the inverse transformation for free by computing its inverse.
Remember, a transformation matrix (linear transformation) \(A\) is applied by doing a multiplication \(A\mathbf x\) where \(\mathbf x\) is a column vector, in this case representing the sequence to transform.
# Use Numpy for linear algebra.
import numpy as np
# Create DFT matrix (square matrix).
# It only depends on size "n".
def create_transformation_matrix(n):
# Based on mathematical definition.
result = np.empty((n, n), dtype='complex_')
w = np.exp(-np.pi * 2j / n)
for i in range(n):
for j in range(n):
result[i][j] = w**(i * j)
return result
Now, here's the code for the actual convolution.
One thing to mention is that it's necessary to pad the sequence with zeros so they are a certain length. Otherwise, the convolution result won't be correct. Since the degree of the product of two polynomials is the sum of the degrees of each polynomial, we set that value as the final length.
def convolution(seq1, seq2): # This is the amount of coefficients the resulting polynomial will have. n = len(seq1) + len(seq2) - 1 # Make both sequences the correct size by adding zeros. seq1 = np.pad(seq1, (0, n - len(seq1)), 'constant', constant_values=0) seq2 = np.pad(seq2, (0, n - len(seq2)), 'constant', constant_values=0) # Build the linear transformation (DFT matrix). matrix = create_transformation_matrix(n) # Find the Fourier transform of both sequences, by applying # the linear transformation (done using matrix multiplication). seq1_dft = np.matmul(matrix, seq1) seq2_dft = np.matmul(matrix, seq2) # Element-wise multiplication. product = np.multiply(seq1_dft, seq2_dft) # Compute the inverse Fourier transform. This is done # by getting the inverse of the DFT matrix, and applying # it as a linear transformation. return np.matmul(np.linalg.inv(matrix), product)
You can verify the results of this function by comparing them against Numpy's convolve function.
Improving Performance Using the Fast Fourier Transform (FFT)
The Fast Fourier Transform (FFT) computes the Fourier transform in \(\mathcal{O}(n\ log\ n)\) time complexity, as opposed to \(\mathcal{O}(n^2)\) (when using the DFT matrix).
It's out of the scope of this article to fully explain how this speedup is obtained. I'm just going to throw some ideas that may give you hints on how FFT is made possible:
- Divide and conquer (divide the polynomial into two halves).
- Recursively compute the Fourier transform of both halves in such a way you can then merge both using some formula.
- Leverage some complex number properties and symmetries to simplify calculations. Some calculations will become unnecessary and can be removed.
- The inverse transform can also be greatly simplified using similar techniques.
Note that for computing a convolution, only the Fourier transform bit is changed. The rest of the algorithm can be kept the same.
Here's an implementation in Python (not micro-optimized). Keep in mind that the sequences now need to be padded with zeros until they are the correct length (i.e., the number of coefficients after multiplication), which in turn has to be rounded up to the next power of two. This is necessary to divide the polynomial into two halves correctly.
def fft(seq, inverse=False):
n = len(seq)
if n == 1:
return seq
w = np.exp(np.pi * 2j / n)
if not inverse:
w **= -1
even = seq[0:][::2]
odd = seq[1:][::2]
a = fft(even, inverse)
b = fft(odd, inverse)
y = np.empty(n, dtype='complex_')
for i in range(n // 2):
x = w**i
y[i] = a[i] + b[i] * x
y[i + (n // 2)] = a[i] - b[i] * x
if inverse:
y /= 2
return y
And there you have it! One of the most important algorithms of all time (perhaps only second to binary search) 😉.
See the Code On GitHub
- Slow convolution (easier to understand, based directly on the mathematical definition)
- Convolution using FFT



