One of the Coolest Convex Hull Problems Ever

Not too Convex Hull is one of the coolest computational geometry problems involving convex hulls I've ever solved.
Given a finite set of \(N\) points, a number \(B\) of polygons to build, and a center \(C\), you must find \(B\) convex polygons having \(C\) as a common vertex such that the total area of all polygons is the smallest possible. Some other important information about the problem:
- All points in the set must either be inside or be a vertex of a polygon.
- Polygons can't overlap or intersect anywhere other than the common vertex \(C\).
- No three points of the set (including the center \(C\)) lie on the same line.
- Very few points, \(N \le 101\).
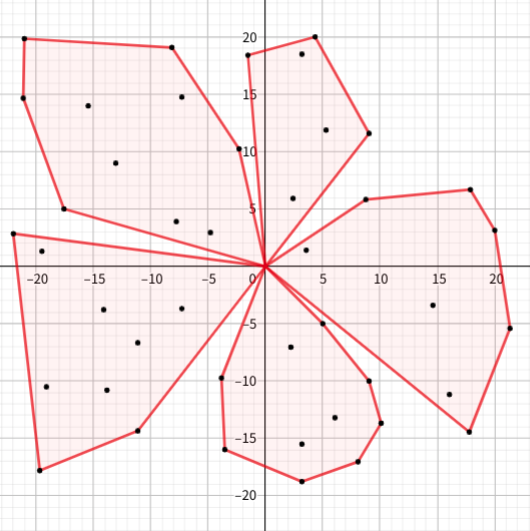
For instance, let \(B = 5\) and \(C\) be the origin, then the figure below shows a possible solution for the point set given. This solution isn't optimal though, as it doesn't have minimum area.
How to Go About It? An Overview of the Algorithm
With experience you can sometimes easily tell whether a problem can be solved using a greedy approach, or with a dynamic programming approach. I chose the latter for this problem, even though I can't really explain the reason, other than that greedy sounds too difficult to get correctly, if possible at all.
Let's imagine we have precomputed all the possible polygons we can build. This means, we know which points they cover, and the area they have. For each starting point \(i\), move counter clockwise and build all polygons that cover from \(i\) to all other points \(j\) until we can't continue enlarging the polygon anymore. At some point the polygon will become concave, so we move on to build polygons that start at \(i + 1\), until we have built all possible polygons. All of this will be explained further in the next section.
All of this can be done in \(O(n^3)\) because building a polygon from \(i\) to \(j\) requires you to traverse all points in between. This can be lowered to \(O(n^2)\) by avoiding doing this and instead using the previous polygon as a starting point to build the next one, but it's a bit harder to implement, and unnecessary for \(N \le 101\) points.
Once all polygons have been precomputed, we can use a knapsack like approach to find the optimal solution. The main idea is that while you are building the solution, if you have placed a polygon that covers all points ranging from \(i\) to \(j\), then for the next polygon you must try all polygons that begin at the \(j+1\) point. Try all of them, and keep the minimum total area at every step. Recursively keep adding the next polygon until you have built all necessary \(B\) polygons, and all \(N\) points have been covered. This will yield the global minimum area once the process is complete.
Using Radial Sweep to Build All Convex Polygons
The Graham Scan algorithm is one of the most common ways to build the convex hull of a set of points. It works by doing a lexicographic sort and the sweep line technique to find both the upper and lower hulls. I recommend to understand how this algorithm works before continuing.
For this problem though, the approach is slightly different. Instead of finding the lower and upper hulls, we center all the points at the given center \(C\), polar sort them, and then use the radial sweep technique to traverse them in counter clockwise order while building each polygon.
Consider the ConvexHull data structure which contains all the essential information about a polygon:
struct ConvexHull {
int start_idx, last_idx, covered;
double area;
};
The following procedure returns a ConvexHull instance by building a polygon from \(i\) to \(j\) travelling counter clockwise. This assumes the points have already been sorted:
ConvexHull create_convex_hull(const int start_idx, const int last_idx) {
int covered = 0;
vector<Point> vertices;
for (int i = start_idx;; i = (i + 1) % N) {
if (vertices.size() < 2) {
vertices.push_back(points[i]);
covered++;
if (i == last_idx) break;
continue;
}
while (vertices.size() >= 2) {
Point a = points[i] - *(next(vertices.rbegin()));
Point b = points[i] - *vertices.rbegin();
if (a.cross(b) > 0) break;
vertices.pop_back();
}
vertices.push_back(points[i]);
covered++;
if (i == last_idx) break;
}
double area = 0;
for (int i = 0; i < (int)vertices.size() - 1; i++)
area += fabs(vertices[i].cross(vertices[i + 1])) / 2L;
return {start_idx, last_idx, covered, area};
}
The process of building all polygons (briefly described in the previous section) can then be done the following way:
vector<vector<ConvexHull>> convex_hulls;
// ....
for (int i = 0; i < N; i++)
for (int j = i + 1;; j++) {
j %= N;
if (points[i].cross(points[j]) < 0) break;
convex_hulls[i].push_back(create_convex_hull(i, j));
}
Finding the Solution Using Dynamic Programming
Finding the minimum area can be done using a pretty standard dynamic programming relation:
double dp(int idx, int b, int covered) {
if (b == 0 && covered == 0) return 0;
if (b == 0 && covered != 0) return INF;
if (b != 0 && covered <= 0) return INF;
if (memo[idx][b][covered] > 0) return memo[idx][b][covered];
double min_area = INF;
for (ConvexHull& c : convex_hulls[idx]) {
double area = c.area + dp((c.last_idx + 1) % N, b - 1, covered - c.covered);
min_area = min(min_area, area);
}
return memo[idx][b][covered] = min_area;
}
This implementation returns \(\infty\) for all invalid configurations. For example, if \(b = 0\) (meaning that we have built all necessary polygons) and at the same time \(covered \neq 0\) (meaning that some points are not covered by any polygon) then the configuration is invalid since some points were left out.
Since we are minimizing at every step, the \(\infty\) values will eventually get replaced by a real number once a valid configuration has been found. In this problem it's guaranteed that a solution exists.
The final solution can then be found using:
double min_area = INF;
for (int i = 0; i < N; i++) {
min_area = min(min_area, dp(i, B, N));
}
Source Code
My C++ implementation of the solution described in this article can be found here.