Shortest Path On a Dynamic Graph

September 3, 2023

Christopher Vilches

Here's a nice little algorithmic problem I solved several years ago. This problem isn't that hard, but it wasn't until recently that I came up with a way to prove that the algorithm works.

The statement of Galactic Taxes can be summarized as follows:

Given a graph in which edges have a cost specified by \(At + B\), find the time \(t\) where the shortest path has the maximum cost. Constants \(A\) and \(B\) are given for each edge.

The source and target nodes are given in the statement.

Value of \(t\) belongs to \([0, 1440]\).

On one hand, we are told that we should always compute the shortest path from source to target. In informal terms, we can say that we should always use Dijkstra's Algorithm (or any other algorithm for computing the shortest path on a graph) for any value of \(t\). On the other hand, we are also told that we should maximize the path cost in function of \(t\).

In this problem, once a path traversal starts, the graph uses the same \(t\) value for the entire path without changing along the way. This makes it a lot easier than it'd be otherwise.

Finding the Highest Value of a Unimodal Function

For this problem, we'll use the ternary search algorithm to find the maximum value. This algorithm finds the minimum or maximum value of unimodal functions by iteratively refining the search space or, in other words, reducing the search interval. We'll use the interval \([0, 1440]\), which is the range of valid \(t\) values.

On each iteration, two values \(t_1\) and \(t_2\) are chosen by the algorithm. We need to calculate the shortest path using Dijkstra's algorithm for both values. Since every edge is defined using the formula \(At + B\), we just need to plug the value into it. Then, the interval is modified in such a way that we get closer to the solution.

Dijkstra's algorithm may be relatively computationally expensive, but the ternary search doesn't need too many iterations and converges quickly. After a few dozen iterations, we'll get a good numerical approximation of the solution.

Sounds good, but how do we know that the function we are trying to maximize is unimodal? In simple words, this would mean the function starts as a monotonically increasing function, then at some point, it becomes monotonically decreasing. This implies there's one global maximum where the function changes from increasing to decreasing.

Proving the Function Is Unimodal

Every possible path in the graph has a cost that can be computed as the sum of the cost of all edges present in said path. Also, remember that each edge \(i\) has a cost defined by \(A_it + B_i\).

For each independent path, the result of \(\sum{A_it + B_i}\) will always be another line since a sum of degree one polynomials always gives you another polynomial of degree one or zero.

We can represent the cost of all possible paths by drawing a bunch of lines. Each line represents the cost of one path in function of \(t\).

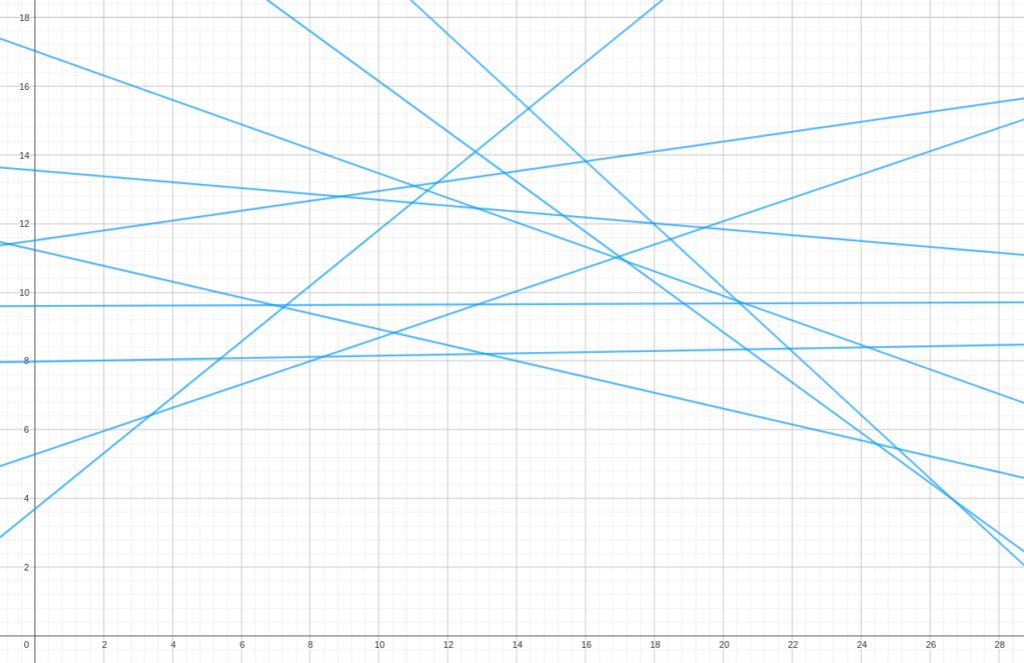
It's important to note that every path computed for any value of \(t\) must be the shortest one. So, going back to our visualization, we can tell we must keep the lower part of the set of lines, so to speak. This resembles a convex polygon (or an upper convex hull).

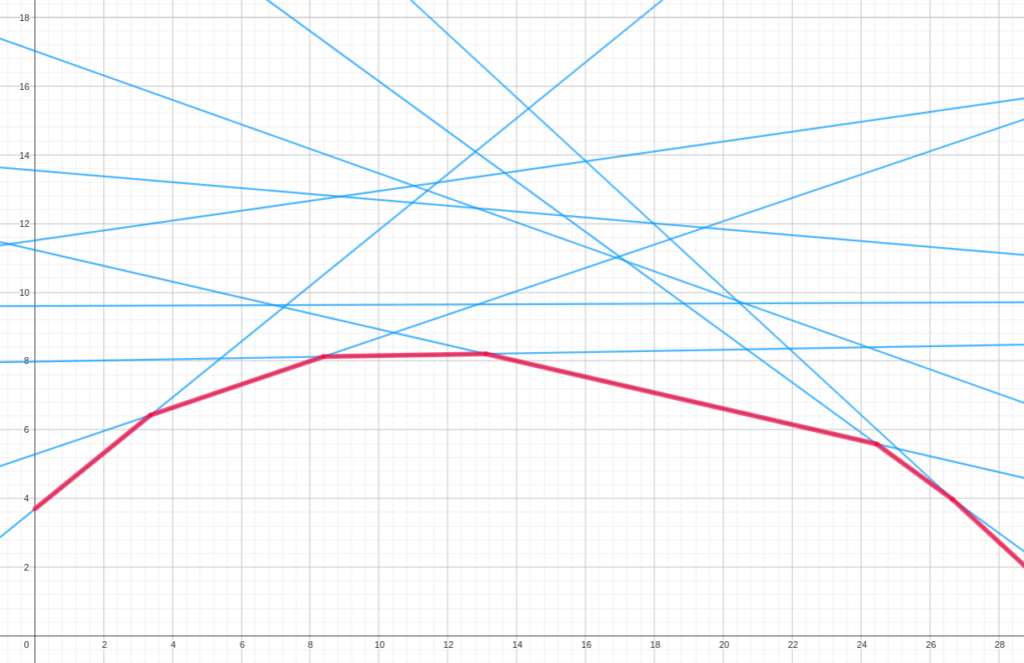
We can clearly see the function is unimodal. However, note that we haven't really proved it yet mathematically. We just visualized it, but this is better than having no proof at all 😉. I guess it can be proved more appropriately with some additional math and/or observations.