(Radial Sweep) Find the Largest Square That Does Not Contain Any of the Given Points

Build the Perfect House is one of the problems that appeared in the ICPC Latin American Regional – 2019 competitive programming contest. It can be summarized as follows:
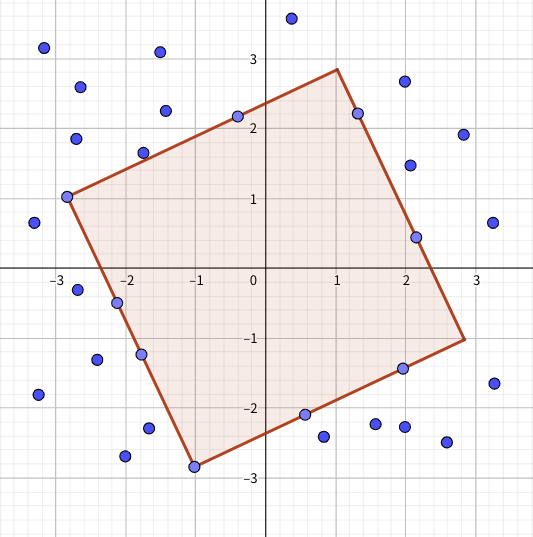
Given a finite set of points, find the square centered in \((0, 0)\) with the largest size that does not contain any of the given points. The sides of the square don’t need to be aligned with the coordinate axes (i.e. the square can be rotated arbitrarily.) Points are allowed right on the border of the square but not inside.
Check out the problem set of the contest.
Algorithm Summary
This is a classic radial sweep problem, in which we fix a square of a certain size, and then rotate it while checking if there's an angle where all points are outside (or right on the border of) the square. The size is then maximized using binary search.
The algorithm is divided into two parts described below.
Radial Sweep
Let \(S\) be an arbitrary fixed square size.
As the square of size \(S\) is rotated on its center, each point will behave in one of the following ways:
- It is always inside, making it impossible to build a square of size \(S\).
- It never touches the square, in which case it can be safely ignored.
- It will enter and then exit the square (or exit and then enter.)
The points that enter and exit the square generate two events:
- Enter event: The point has entered the square.
- Exit event: The point has exited the square.
These events are all put into a single array and then sorted by angle. Performing a radial sweep essentially means iterating over these events in order. This is the equivalent of rotating the square on its center and having points enter and exit the square at different angles. By using a simple counter variable it's possible to keep track of how many points are inside the square at any given rotation.
To summarize:
- Generate all events for all points.
- Sort the events by angle.
- Process all events in order by making the square rotate on its center.
- It's possible to build the square if there's at least one moment where there are no points detected to be inside the square.
- If there are no moments where there are no points inside, then it's impossible to build.
This process returns a boolean, which indicates whether it's possible or not to build a square of size \(S\).
Binary Search
The process above must be executed multiple times for many \(S\) values using binary search. This will yield the highest \(S\) such that a square of that size can be built without having any point inside.
Note: \(S\) can be the side, diagonal, area, etc. Since it's a square, all these measures are proportional to each other, so you can use whatever you want.
Analysis
A Few Observations
- Rotating all the points until they are in the first quadrant does not change the final answer: Because squares are symmetric, we can just put all points in the first quadrant. Simply rotate each point \(90^{\circ}\) a few times until they are all in the first quadrant.
- We can ignore a point if its distance to the origin is greater than the square diagonal: No matter how we rotate the square, the point will never enter the square, so these points can be ignored.
- If at least one point is inside the circle inscribed inside the square, then the square can never be built: In other words, if a point's distance to the origin is less than half of the square side, then no matter how we rotate the square, that point will never exit it.
- A square can only be rotated \(90^{\circ}\): Again, because the square is symmetric, we only have to rotate it \(90^{\circ}\). No new information will be gained by rotating it further.
Moreover, if we consider all the points that were not ignored (i.e. points that lie outside the circle inscribed inside the square, and which distance to the origin does not exceed the square diagonal), then we can also make the following observations:
- After the square has been rotated by \(90^{\circ}\), if the point was initially inside, then it will exit once, and then re-enter.
- Similarly, if the point was initially outside, it will enter the square, and then exit again.
- As a conclusion, all non-ignored points have two events.
The proof is that after rotating the square \(90^{\circ}\), the final state will be the same as the initial state (due to its symmetry). This means that all points that were initially inside, will end up being inside when the \(90^{\circ}\) rotation ends, but it also means that the point had to exit the square once and then enter again. This proof also applies for points that were initially outside the square.
Calculating the Events Associated to Each Point
In some radial sweep implementations, events are specified as angles, but the most common way to implement it is by simply using points as events, which is what we are going to do here.
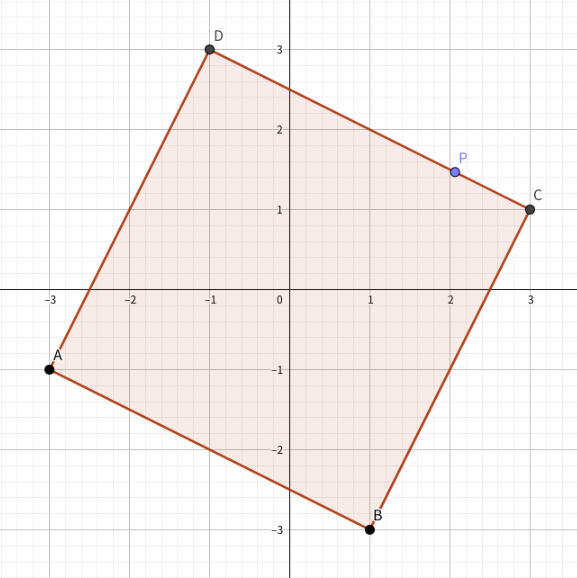
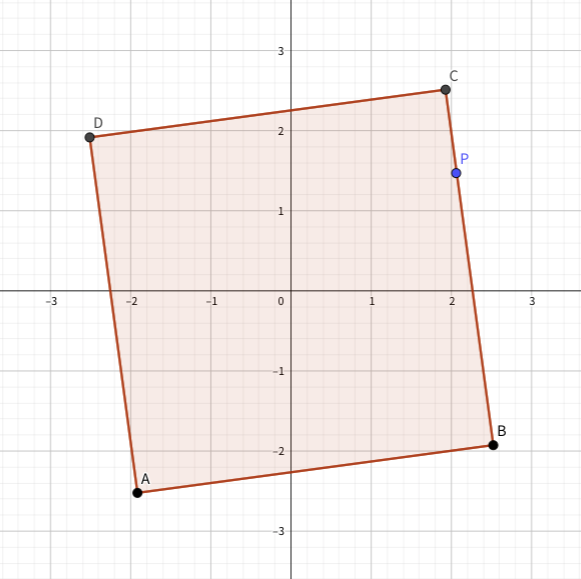
The way I approached the radial sweep is by having the square's initial state be in such a way that the four vertices lie on the coordinate axes, and rotate it all the way until (as pointed out above) the final position is the same as the initial one.
You can visualize this algorithm as sweeping the rightmost vertex (labelled C in the figure below), passing through all the events, and finally arriving at D.
For this reason, the easiest way to transform each point into an enter or exit event, is by executing the following:
- Let \(P\) be the point you are currently handling, \(S\) be the length of the square side, and \(I\) be the circle inscribed inside the square.
- Obtain the two points of tangency from \(P\) to the circle \(I\) (there are always two).
- From each point of tangency \(T\), obtain the vector \(\vec{TP}\), normalize it, and scale it by \(\frac{S}{2}\). Keep the vector's endpoint. This is the point that represents the angle at which the square vertex is located when \(P\) enters/exits the square.
The last bit is a bit tricky to do correctly, and for me the easiest way was to simply get all four possible points (see the code for more details), get the ones in the first quadrant, and then sort them radially so I can tell which one is the first and last one to be visited during the radial sweep. The expected result is that you should end up with two points, both in the first quadrant, and know which one goes first during the sweep.
Also, in order to know whether the first event should be enter or exit you only need to check whether the point is below or above the square side (segment from D to C in the figure). Using the line equation helps:
$$y = mx + b$$
Implementation in C++
Use Long Double
Just to avoid confusions, ld means long double here.
typedef long double ld;
Polar Sort
Sort the points by bearing by implementing a Point struct with a operator< comparator. Note that this comparator does not work when some points are \(180^{\circ}\) or more from each other, but in this program all points are in the first quadrant, so it works fine.
struct Point {
ld x, y;
// ...
ld cross(const Point& p) const { return x * p.y - y * p.x; }
bool operator<(const Point& p) const { return cross(p) > 0; }
// ...
};
Radial Sweep
The next snippet shows how the radial sweep was implemented in my solution.
Binary search is used in order to find the optimal value for the \(possible(S)\) function. Check out the full C++ solution.
bool possible(ld side) {
ld half_side = side / 2L;
ld half_diagonal = half_side * sqrt(2);
// Store the events here as a Point/boolean pair
// The Point is for specifying the event position,
// and the boolean means enter (true) or exit (false)
vector<pair<Point, bool>> events;
// Counter for keeping track of how many points are currently inside the square
int inside = 0;
// Generate all events
for (Point& p : points) {
// Is the point always inside the square?
if (p.magnitude() < half_side) return false;
// Should we ignore the point because it never enters the square?
if (p.magnitude() > half_diagonal) continue;
// Points of tangency from p to the inscribed circle inside the square.
auto [t1, t2] = points_of_tangency(half_side, p);
// Vectors that reach a square vertex when added to the points of tangency.
Point u = (p - t1).normalize().scale(half_side);
Point v = (p - t2).normalize().scale(half_side);
// Radial sweep is [0, 90] degrees, so find the ones in the first quadrant.
Point event1 = (t1 + u).is_first_quad() ? (t1 + u) : (t1 + u.negate());
Point event2 = (t2 + v).is_first_quad() ? (t2 + v) : (t2 + v.negate());
// Order the events
if (event2 < event1) swap(event1, event2);
bool point_initially_inside = p.y < half_diagonal - p.x;
// When it starts inside the square, it will exit and then enter again.
// When it starts outside the square, it will enter and then exit.
if (point_initially_inside) {
inside++;
events.push_back(make_pair(event1, false));
events.push_back(make_pair(event2, true));
} else {
events.push_back(make_pair(event1, true));
events.push_back(make_pair(event2, false));
}
}
// If there are no events, it means that all points were ignored.
// The square can be built.
if (events.empty()) return true;
// Execute a polar sort. Use the Point comparator defined in the struct.
sort(events.begin(), events.end(),
[](const pair<Point, bool>& a, const pair<Point, bool>& b) {
return a.first < b.first;
});
// It's possible to build the square if there's at least one rotation with no
// points inside.
// Radial sweep of square diagonal, from 0 to 90 degrees.
for (pair<Point, bool> ev : events) {
// We don't need the point here. It's only used for sorting.
auto [_, enter] = ev;
// Keep track of how many points are inside
inside += enter ? 1 : -1;
// If no points are currently inside, then it can be built.
if (inside == 0) return true;
}
return false;
}


