Sorting the Unsortable: A Sweep Line Algorithm for Partially Ordered Segments

Here’s a nice algorithm that I learned a few years ago. Given a set of non‑intersecting slanted segments, determine the order in which to traverse them from highest to lowest, following the natural flow along their slopes.

This algorithm can be used to solve some interesting problems, like finding the sequence in which something flows when being dropped from above, letting gravity make it follow the slopes of each segment. Something like in the following picture:

In this article, we explore the difficulties of ordering this kind of data and how we can represent the ordering by building a tree instead of a list.

This algorithm is based on the sweep line technique, but it also incorporates concepts from graph theory.

We’ll be considering only non-vertical segments, either slanted or horizontal, and without any intersection between them, not even at their endpoints.

By the way, this post’s title was generated by an LLM. I think it’s corny as hell, but I kind of liked it anyway, and it’s better than anything I could come up with myself.

Let’s dive right in, but not without first taking a look at the rather annoying concept of posets.

Partially Ordered Sets (Posets), or Why Not Everything Can Be Ordered

A partially ordered set (poset for short) is a set where not every pair of elements has a greater than (or less than) relation. The basic idea is that for some pairs of elements, you can tell whether one element is less than the other, but for other pairs, the elements are neither less than nor greater than each other.

Mind that this is going to be a very informal explanation of posets. If you want to learn it in more detail, I’d recommend finding a more in-depth resource.

If you have a list or set of unique numbers and you pick two random elements, there will always be a clear way of knowing which one is the greater element. For example, 2 is less than 5, -1 is greater than -100, and so on.

However, there are times when two elements have no clear way of deciding which one is the greater element. A common scenario is task scheduling: imagine a set of tasks where some tasks must be completed before others, but many tasks are independent. For example, “compile source code” must happen before “run tests,” but it may have no dependency on “write documentation.” These unrelated tasks have no defined order in the poset, so for some pairs, there’s no way to decide which one goes first.

Comparing and Ordering Segments

Take a look at the following picture. If you were to decide which segment is above the other, which one would you pick? The correct answer is: there’s no segment above nor below, as they shouldn’t even be comparable.

One reason why we shouldn’t even bother comparing these two segments is that their ordering gives us nothing useful for what we are trying to do. Remember, we are trying to decide what would happen if we drop something from above and simulate the flow or movement it undergoes by following the slopes. Since these two segments aren’t horizontally overlapping, the object will never fall off from one segment to the one below.

Turns out we should only consider two segments as comparable if they are horizontally overlapping, such as in the figure below. An object being dropped over the upper segment will eventually fall into the lower one due to gravity when following the slope. The segment that leads into the other one is the one considered above, and the one that receives the object is the one below. The comparison can be implemented using some simple geometric checks, such as the right-hand rule or the dot product.

Representation Using Directed Acyclic Graphs

Posets can be conveniently represented using graphs, specifically directed acyclic graphs (DAG for short). Basically, whenever an element is less than another element, we connect them by an edge from the smaller element to the larger one. We don’t connect a pair of elements that have no relative order between them, and we also don’t need to connect all elements if we can infer the order via transitivity, that is, by following a path of edges.

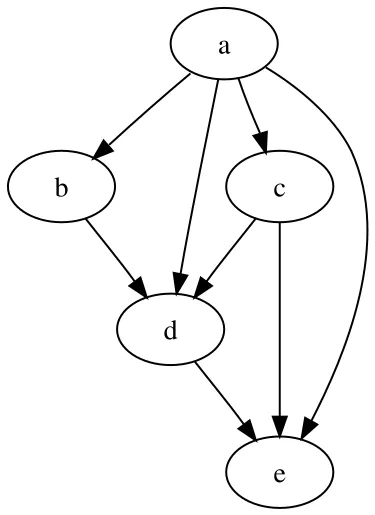
One mistake I’ve made in the past is trying to run a sorting algorithm on a list of elements from a poset. This doesn’t work because not all pairs of elements are comparable, so a standard sort cannot produce a meaningful total order. Instead, the data must first be stored as a DAG representing the partial order, and then a topological sort can be used to produce a valid linear order when needed.

For a similar reason, it also doesn’t make sense to store poset elements in an ordered set (i.e., TreeSet) since the order would eventually break. However, you actually can do it safely if you make sure that, at any given time, only comparable elements coexist in the set, and this is actually an important part of my implementation, which will be explained in a bit.

When outputting the result of the toposort, any higher segment will always appear before the segments below it. For segments that are not comparable, their relative order is arbitrary, since it doesn’t matter which one comes first.

Even though DAGs are the generic way to represent posets, this algorithm actually represents the data using just a tree, which is a specific type of DAG.

Implementing the Algorithm

Having explained the caveats related to how segments can be sorted, let’s go back to the main algorithm.

The algorithm is fairly straightforward, but I’m going to skip some implementation details, such as building graphs and the algorithm for computing topological sorts on DAGs.

The core steps of the algorithm are as follows:

1. Implement a comparator: Assume the two arguments (i.e., elements being compared) are already horizontally overlapping. Then implement a geometric check to know which one is above (e.g. right-hand rule).
2. Sweep through the segments: Traverse all segment endpoints, both left and right, in ascending order of their x-coordinates.
3. Handle segment enter event: When the sweeping line enters a segment from its left, add it to an ordered set (using the custom comparator), and add an edge from the previous element in the set to the newly added one.
4. Handle segment exit event: Similarly, when the sweeping line exits a segment from its rightmost endpoint, remove it from the set.
5. Topological sort: Perform a topological sort on the graph you built.

The output should be a 1-dimensional array containing a valid topological sort of the segments, ordered from higher to lower.

Why do we remove segments from the set? The comparator I implemented for the segments assumes that all segments currently in the set are horizontally overlapping, making them mutually comparable. Therefore, it is crucial to remove a segment from the set as soon as the sweep line passes its rightmost x-coordinate. Beyond that point, some segments will no longer overlap, and some pairs of elements will no longer be comparable.

Note that because some segments have no segment above them, you can just use an imaginary node representing an infinitely high segment, which is above all other segments in the set. This node is actually the root of the tree.

The resulting graph is actually just a tree, and we know its root, so the topological sort is much easier to compute.

As a side note, an edge between two segments is only added if the upper segment’s leftmost endpoint has a smaller x-coordinate than the lower segment’s. This happens because the sweep line processes segments from left to right, and an edge is only created when the upper segment is already in the active set as the sweep line reaches the lower segment. If the upper segment starts further to the right, it will not be in the set at that moment, and the lower segment will instead be linked to another segment (or the imaginary ceiling).

There’s a smart trick we can use to handle this. We can simply output the topological sort in reverse child order, listing each node’s rightmost children first. This approach favors the edges that were actually discovered, and for any missing edges, the final topological order naturally reflects the order those edges would have implied if they existed. This trick does not affect correctness because a topological sort ends up flattening the graph anyway, so the exact structure of intermediate edges is not required for the final ordering. I know, it’s kind of weird, but this hack, along with the transitivity property, makes this algorithm require way fewer edges than it otherwise would. Alternatively, if you still need the full graph, you can modify the algorithm above to add all the necessary edges.

Practice Problems

I didn’t find many problems that use this algorithm, but here are the ones I know and have solved with it:

• Pinball: After the segment sorting, the remaining logic is very simple. My solution is here.
• November Rain: Classic problem. Intermediate difficulty.
• Directing Rainfall: Very hard. Sorting the segments is barely half of the solution.